This topic applies to several software solutions that are aimed at the general 3D production industry, such as Max, Maya, Blender, Zbrush etc.
These programs allow the user to load and edit STL files. So it is possible not only to see the model, but also to edit and retopologise it.
The problem with STL format is that meshes get triangulated when saved, so it is complicated for designers when they try to edit them because that is not very topology-friendly. However, if the original designer defined a good layout, the original topology can be recovered (at least in Blender) with an algorithm so that it can be worked on more easily.
What is the topology of a mesh?
As we all know, 3D models are composed of meshes. These meshes contain vertices, edges and faces. With them, we define the geometric shape of a surface.
The layout that defines the relationship between vertices, edges and faces is what we call the topology of a model.
When discussing the different faces of a mesh, the literature usually distinguishes three types: polygons with 3 faces (tri), with 4 faces (quad) or with more than 4 faces (n-gon).
The topology of a mesh studies the type of polygons that are used to constitute the mesh, but also how they are related to their neighbours to adjust to the curvature of the surface and the composition of closed loops within it.
Why learn about topology?
When we export meshes for printing, they usually end up triangulated, even though this did not form part of our original design.
It might seem that in this specific scenario it is irrelevant whether we choose one type of topology or another as long as the surface adapts to the shape we want to give the object. This is not necessarily true.
While the main goal of a printable model is to be printed, there are three key benefits that topology can bring:
- Good topology adds quality to the curvature of the model’s surface, which is especially relevant in high-detail printers.
- It is a good practice that makes it easy to make changes to the 3D mesh to adapt it to other needs.
- It allows delivery to the consumer of a low-poly model that is user-friendly with the application of subdivisions to enlarge the detail, which implies smaller file sizes.
However, it is important to keep in mind that maintaining good topology in our models is a task that takes time and practice. There will be situations where it is simply not worth it and, as designers, we must be able to identify them.
Learning to distinguish good topology from bad
There are many criteria that define good practice when designing our topology.
As far as the type of polygons is concerned, we should try to avoid using tris and n-gons as much as possible. When trying to subdivide a mesh, these types of polygons usually do not subdivide well. In addition, only the quads generate closed loops of edges that facilitate cutting and bevelling.
An easy way to visually detect defects in the mesh surface is to see if it produces pinching effects. This pinches are usually produced either by a concentration of a high number of faces in a concrete region of the surface or due to vortices. A vortex is a vertex that receives more than 4 edges.
The defects tend to be more noticeable as the resolution of the mesh increases. Try subdividing it several times and see how it deforms.
Good topology adapts by folding over its edges in the areas of maximum concavity or convexity.
A loop is a sequence of 3 or more consecutive quads that close forming a ring. Edge loops can be used to define the compression of surfaces. If harder edges are needed, more loops should be put closer together.
It is also very useful to review the normals. A normal is the orthogonal vector to a plane defined by the vertices of a specific polygon.
On curved surfaces, it is important that there are no sudden changes of shape and normals between neighbouring polygon areas. However, on flat surfaces, this is usually less important because all the of those surfaces point in the same direction.
T-shaped vertices, internal faces or unconnected areas should be avoided.
Take into account the density of polygons. The areas with more curvature will require a greater number of polygons. Flatter areas need fewer polygons.
Solutions to topology problems
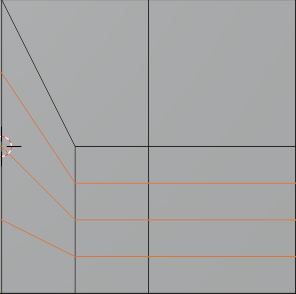
Despite the previous recommendations, and especially in organic modelling, it is very common to find situations in which we must connect an area that contains, for example, 5 loops with another with only 3, while still trying to maintain a quad-type polygon structure.
Below we show some of the most common situations. The way to read it is from left to right or from right to .
Special care must be taken with (C) since it is the only one that is not symmetrical. If new loops are created horizontally, this solution can either load all cuts into one half or change the flow direction of the edges.
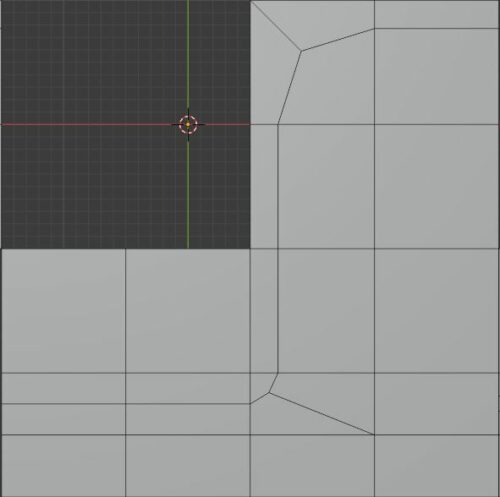
If what we want is to redirect the direction of a loop, we can use the following trick:
We start by dividing a quad into 4 sections and then cut as shown in the following image. The result will generate a tri and an n-gon.
We subdivide the edge connecting the tri to the n-gon and then connect it to the opposite vertex.
We can then perform the same exercise to reorient the curvature of that surface in another direction.
That curve can be bevelled and even closed using the technique (B) described in this section.